Secondary Focal Point of a Dome Port

The diagram below shows a concentric spherical dome port with outer and inner radii r1 and r2, respectively. When it is used (as shown) to form an interface between water and air it acts as a diverging lens. A distant point object on the dome's optical axis, when viewed from the air side of the dome, will appear to be situated at F", the dome's 'secondary focal point'. Since none of the light coming from the point object and refracted by the dome ever physically passes through point F", the image is referred to as virtual, instead of real.

The position of the secondary focal point, i.e. the position of the 'infinity' virtual image, is an important consideration when matching a camera lens to a dome port. For example, if a properly positioned camera lens cannot focus closer than point F" it will be necessary to add a corrective lens (diopter) that will allow closer focus. To get the widest range of focus, the optimal diopter to use is the one that places the far plane of focus at or slightly beyond point F". For that, you need to know where F" is situated.

The distance from F" to the external vertex of the dome (point A in the diagram) is given exactly by the formula

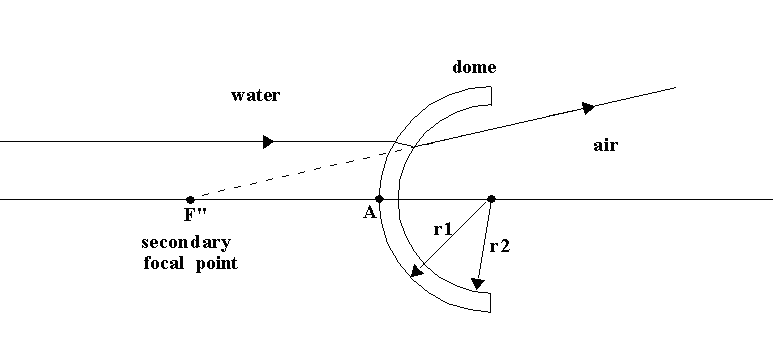
AF" = -r2*[n"/(1-n)]*(1-g)/[1 - g/(1-n)] - (r1-r2)         Equation 1

where

          g  = [(n'-n)/n']*(r1-r2)/r1
          n  = index of refraction of water
          n' = index of refraction of the dome material
          n" = index of refraction of air

Putting n"=1 and n=4/3 (this is accurate enough for our purposes), get

AF" = 3*r2*(1-g)/(1+3g) - (r1-r2)                           Equation 2

with

          g = [1 - 4/(3n')]*(r1-r2)/r1

Typically, the value of g is of the order 1/100, so we can write, to an excellent approximation (error = .03%)

AF" = 3*r2*(1-4g) - (r1-r2)                                 Equation 3

Equations 1 and 2 are exact, and Equation 3 is nearly exact, but neither can serve as a simple rule of thumb for locating the infinity virtual image. To find a simple rule we must make a few simplifications. First, we note that the dome's index of refraction is typically in the range 1.5 < n' < 1.6, and over this range the right hand side of Equation 3 is a weak function of n'. So, accuracy will not suffer much by putting n'=3/2. Next, express r1 and r2 in terms of the mean dome radius
R=(r1 + r2)/2 and the dome thickness t = r1 - r2:

            r1 = R + t/2
            r2 = R - t/2

Substituting for n', r1, and r2 in Equation 3, expanding in powers of the small quantity t/R, and keeping only the zeroth-order terms, we get

AF" = 3R - 4t + 5t/18                                       Equation 4

or, since the 3rd term is small compared to the 2nd term, the very simple result

AF" = 3R - 4t                                               Equation 5

The table shown below compares the results from Equation 2 (exact), Equation 3 (almost exact), and Equation 5 (rule-of-thumb) for several dome indices of refraction and dome radii. All distances are given in inches. Note that the rule-of-thumb formula is usually accurate to within one or two tenths of an inch!!

The rule-of-thumb for locating the infinity virtual image is therefore: " three radii minus four thicknesses from the front of the dome"

                                       DOME TO VIRTUAL IMAGE     
                                     ------------------------
                                              almost    rule
                                      exact    exact     of
            n'    r1     r2      t   (Eq.1)   (Eq.2)    thumb
                                     ------------------------

          1.50  2.500  2.375   .125   6.84     6.84     6.81
                       2.250   .250   6.21     6.20     6.13          
                       2.125   .375   5.60     5.57     5.44
                       2.000   .500   5.00     4.97     4.75
                3.000  2.875   .125   8.34     8.34     8.31
                       2.750   .250   7.70     7.69     7.63
                       2.625   .375   7.08     7.06     6.94
                       2.500   .500   6.47     6.44     6.25
                3.500  3.375   .125   9.84     9.84     9.81
                       3.250   .250   9.20     9.19     9.13
                       3.125   .375   8.57     8.55     8.44
                       3.000   .500   7.95     7.93     7.75
                4.000  3.875   .125  11.34    11.34    11.31 
                       3.750   .250  10.69    10.69    10.63
                       3.625   .375  10.06    10.05     9.94
                       3.500   .500   9.44     9.42     9.25

          1.55  2.500  2.375   .125   6.80     6.80     6.81
                       2.250   .250   6.14     6.12     6.13          
                       2.125   .375   5.50     5.47     5.44
                       2.000   .500   4.88     4.83     4.75
                3.000  2.875   .125   8.30     8.30     8.31
                       2.750   .250   7.63     7.62     7.63
                       2.625   .375   6.98     6.95     6.94
                       2.500   .500   6.35     6.30     6.25
                3.500  3.375   .125   9.80     9.80     9.81
                       3.250   .250   9.12     9.11     9.13
                       3.125   .375   8.46     8.44     8.44
                       3.000   .500   7.82     7.78     7.75
                4.000  3.875   .125  11.30    11.30    11.31 
                       3.750   .250  10.62    10.61    10.63
                       3.625   .375   9.95     9.93     9.94
                       3.500   .500   9.30     9.27     9.25

          1.60  2.500  2.375   .125   6.77     6.76     6.81
                       2.250   .250   6.07     6.05     6.13          
                       2.125   .375   5.41     5.36     5.44
                       2.000   .500   4.77     4.70     4.75
                3.000  2.875   .125   8.27     8.26     8.31
                       2.750   .250   7.56     7.54     7.63
                       2.625   .375   6.88     6.84     6.94
                       2.500   .500   6.23     6.17     6.25
                3.500  3.375   .125   9.76     9.76     9.81
                       3.250   .250   9.05     9.04     9.13
                       3.125   .375   8.36     8.33     8.44
                       3.000   .500   7.70     7.64     7.75
                4.000  3.875   .125  11.26    11.26    11.31 
                       3.750   .250  10.55    10.53    10.63
                       3.625   .375   9.85     9.82     9.94
                       3.500   .500   9.18     9.13     9.25