The west coast of Bonaire. July. Socrates is gazing out to sea while expounding on the meaning of life, absolute beauty, the immortality of the soul, and why there are so many donkeys on Bonaire. Plato interjects:
Plato: "How far away do you think that plane is?"
Socrates: "What plane?"
Plato: "See that light just above the horizon? That’s ALM flight 122 coming in from Curacao. Late, as usual."
Socrates: " Yes, I see it. But if it is usually late, then it must be on time. Do you know the wing span?"
Plato: " That is well and truly said, Socrates. Zeno’s paradoxes pale in comparison to yours. I think it’s a de Havilland Turbo Dash 8, so the wing span is probably about 90 feet".
Socrates: "If we wait until the plane is closer, I will tell you how far it is."
Plato: "What do you mean, Socrates?"
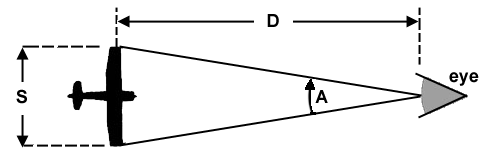
Socrates: " There is a light at the tip of each wing, but the plane is so far away that it looks like only one light. As the plane approaches and that one point of light separates into two points of light, I will know that the plane is just barely at the limit of resolution of my eyes. The best that my eyes can do, and probably yours too, is to resolve about 4 minutes of arc. I can then use the formula for the length of an arc in terms of its radius of curvature and the angle it subtends at its center of curvature. Here, look at this drawing:

If the distance to the plane, D, is large in comparison with the distance S separating the lights, then D is approximately equal to S/A, if A is expressed in radians. So if I know the wing span, I can calculate the distance to the plane using the formula
D=0.65*S/A miles,
where S is in feet and the angle A is now expressed in minutes. When I first see two lights, A will equal 4 and the plane should be about 15 miles away."
Plato: " I think, Socrates, that the harmony in your logic is equal to that in your soul. But let me ask you this: what if the plane is closer than that, and you cannot use the limit of resolution trick? What then?
Socrates: " That’s easy! See that setting sun? It spans about 32 minutes of arc. Just estimate what fraction of the sun’s diameter the wing span occupies, and then multiply by 32. Use that number for A in the formula I just gave you."
Plato: " You are wise, Socrates. But can you explain why there are so many donkeys on Bonaire?"
Socrates: " Pass the hemlock."