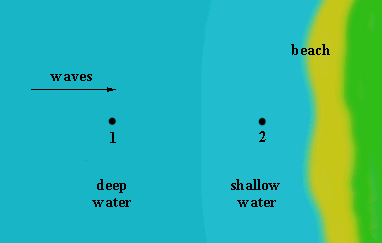

As they arrive at point 1 in deep water, their period is T1. If you count the number of crests that pass point 1 during some interval 'dt', you should get the number
n1 = dt/T1 Equation 1
Suppose now that the wave period changes to the value T2 as the waves approach position 2 in shallower water. The number of crests passing point 2 in time dt is therefore
n2 = dt/T2 Equation 2
The number of waves that have accumulated within the region between points 1 and 2 is the difference between the number entering the region and the number leaving the region, i.e.
# of waves accumulated = n1 - n2 = dt*{1/T1 - 1/T2} Equation 3
Since the time interval dt is completely arbitrary, let it approach infinity.
This makes the number of waves accumulated approach either plus infinity (for T1 < T2)
or minus infinity (for T2 < T1). Neither result is physically acceptable. Hence, our
original assumption that T1 and T2 are different must be invalid. This is a
Conclusion: the wave period is independent of the water depth
A. T. Ippen, "Estuary and Coastline Hydrodynamics" (McGraw-Hill, New York 1966),