A bit of physical reasoning should convince you that this must be true. First, recall two familiar properties of water: (i) it has virtually no resistance to lateral (shear) forces at its surface (for example, however gently you blow across the surface of water, it will move), and (ii) it is very nearly an incompressible fluid --- it is very difficult to force water molecules closer together. Now consider a thin square horizontal slab of water with vertical sides which is embedded within a larger body of water, as shown in Figure 1.
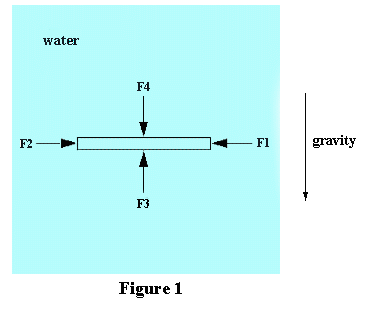
Assume static equilibrium, i.e. no part of the water is in motion relative to any other part. Lack of resistance to shear (property (i)) implies that the external force on each slab face must act in a direction perpendicular to that face. If this were not so, there would be a shear stress across the slab face and it would move, which would contradict the assumption of static equilibrium. The forces on the slab faces are therefore as shown in Figure 1. Not shown are the two other forces which act on the slab edges that are in the plane of the figure.
Continuing with the requirement for equilibrium, it is clear that opposing horizontal forces, such as F1 and F2 must be equal in magnitude. Otherwise the slab would move sideways. Moreover, there is nothing special about the directions of F1 and F2. By symmetry, if you rotate the slab to an arbitrary new position in the horizontal plane, the new lateral forces on the slab edges must be the same as before. This also follows from the incompressibility of water (property (ii)): squeezing the slab in one direction will make it bulge in the other direction until all forces are balanced.
Conclusion: the horizontal forces (and pressures) acting at a point from any direction must be identical in a static fluid.
What about vertically? If the gravitational acceleration were not shown in Figure 1, you could imagine that you were looking down at the slab, and then use exactly the same arguments to prove that F3=F4=F1=F2 (the reasoning did not depend on slab shape!). So let's remove the complicating effect of the gravitational acceleration: let the thickness of the slab approach zero! This forces the mass of the slab, and therefore the gravitational force on it, to both approach zero, and allows us to exploit the symmetry of the situation. Finally, letting the length and width of the slab also approach zero gives us: the pressure at a point in a static body of water is exactly the same from all directions.
There is also a simple, yet elegant, mathematical proof of the above. Consider the water-filled vessel shown in Figure 2, and imagine a prism-shaped element of water (as shown).
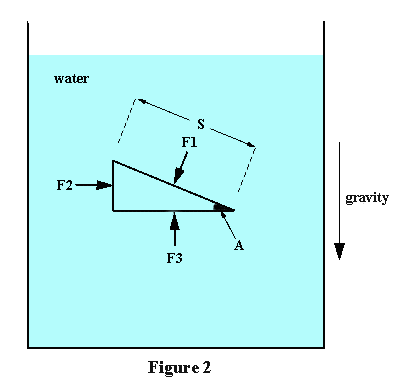
The prism's slanted side has length S, is inclined at the angle A, and the prism has length L in the direction perpendicular to the plane of the figure. As before, static equilibrium requires that the forces on the prism faces be perpendicular to the faces. Using the notation in Figure 2, translational equilibrium in the horizontal direction requires that: