We know from the history books that many ancient sailors were terrified that sailing in one direction towards the unknown would lead them to the edge of a flat earth. Those sailors should have known better. After all, they must have been aware that when a ship sails away it gradually "sinks" below the horizon, and when it returns it gradually "rises" out of the ocean. A strong clue that the earth’s surface is curved.
Since we know about the curvature, we can use it to answer some simple questions, like "how far can you see?" and "how far away is that boat?". If you’re not a sailor, some of the answers might be surprising. For example, the phrase "beyond the horizon" is often used in the context of expressing a vast distance. For a person standing at sea level, however, the horizon is only about 3 miles away.
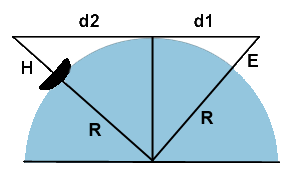
Let’s do the calculations. The figure below shows an observer whose eyes are a distance "E" above sea level.

A straight line drawn from the observer’s eyes tangent to the sea’s surface "touches" it at the distance d1, which is the distance to the horizon. If R is the radius of the earth, then, to first order in E/R, it is easy to show that
![]()
Now suppose that there is a ship beyond the horizon which extends a height H above sea level, as shown. How far beyond the horizon must it sail before it disappears from view? That will happen when the perpendicular to the sea’s surface intersects the previous tangent line at a height H. This occurs at the distance d2 beyond the horizon, where
![]()
With E and H expressed in feet, and d1 and d2 in miles, the above formulas simplify to:
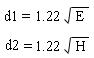
The table below shows the results for some representative values of E and H.
E eye-height(feet) |
H boat-height(feet) |
d1 eye-to-horizon(miles) |
d2 horizon-to-boat(miles) |
d1+d2 eye-to-boat(miles) |
| 0 | 20 | 0 | 5.5 | 5.5 |
| 0 | 40 | 0 | 7.8 | 7.8 |
| 0 | 60 | 0 | 9.5 | 9.5 |
| 6 | 20 | 3.0 | 5.5 | 8.5 |
| 6 | 40 | 3.0 | 7.8 | 10.8 |
| 6 | 60 | 3.0 | 9.5 | 12.5 |
10 |
20 | 3.9 | 5.5 | 9.4 |
| 10 | 40 | 3.9 | 7.8 | 11.7 |
| 10 | 60 | 3.9 | 9.5 | 13.4 |
Note that for E=0 (eyes at sea level) the observer is at the horizon, and for someone who is 6 feet tall the horizon is 3 miles away. That same six-footer will continue to see a 40-foot tall boat until it’s about 11 miles away.
The foregoing assumes a perfectly calm ocean. For a ship on top of a wave crest one must use it’s "effective" height above sea level, namely H plus one wave amplitude.