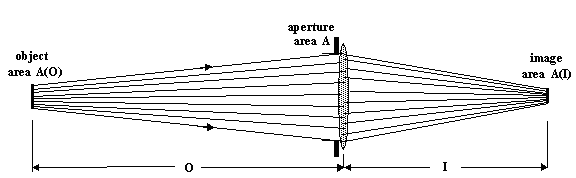

The brightness of the object is given by its luminance B, which is related to the visible light power emitted per unit surface area per unit solid angle. The solid angle subtended by the aperture at the (small) object is A/O^2 (the caret indicates exponentiation). The total power passing through the aperture is therefore (luminance) times (object area) times (solid angle subtended by the aperture), which is
Assuming no attenuation of light along its entire path from object to image, the power arriving per unit area of image, i.e. its illuminance E, is therefore
(The illuminance multiplied by the camera shutter speed is what determines film exposure.) If the magnification ratio is M, then A(I)/A(O)=M^2, and so
But from the thin lens formula, 1/O+1/I=1/F, and the fact that M=I/O, we can easily show that
Using this and substituting A=(pi)D^2/4 , the last expression for illuminance becomes
where pi=3.1.4159... and
For a given object brightness, the film exposure depends on the quantity f, which is known as the f-number. Note that the f-number is a function of the ratio F/D and the magnification ratio. For small magnifications the f-number approaches the value F/D, which is the lens f-stop, and is the number printed on your lens barrel in the typical sequence 2.8, 4, 5.6, 8, 11, etc.
For close-up photography, however, M is not small. Suppose that for some small value of M you have determined the f-number required for perfect film exposure and that you have set the size of the aperture accordingly. As you now bring the object closer, while keeping it in focus, the magnification ratio will increase and the image illuminance will decrease. To avoid underexposing the image you must therefore increase the size of the aperture to restore the f-number to its required value.
Note that the illuminance is inversely proportional to the square of the f-number. Doubling the value of f decreases the illuminance by a factor of four. Since it is convenient to work with illuminances that differ by factors of two, f-stops are usually chosen so that the ratio of consecutive values equals the square root of two.
REFERENCE:
F. A. Jenkins and H. E. White, "Fundamentals of Optics" (McGraw-Hill 1957), Chapter 10.