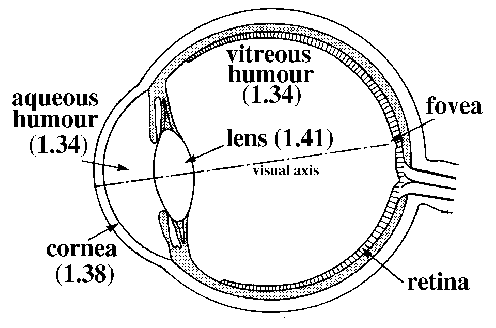
While in contact with air, the normal human eye does a wonderful job of feeding accurate visual information to the brain. In contact with water, however, it fails miserably. To understand why, we need to examine the eye's optical properties. The figure below shows a lateral cross-section of the human eye (taken from Hallett et al). The number accompanying the label of each eye component is its index of refraction. In particular, note that the index of refraction of the cornea, n(c), is 1.38.

The refractive power of the cornea when it is in contact with air (which has index of refraction n(a)=1.00) is
P(a)={n(c)-n(a)}/R
where R is the cornea's radius of curvature. If the radius is expressed in meters the unit of power is the diopter. Typically we have R=0.008 meters. Substituting the known values into the above equation produces
P(a)=47.5 diopters.
If, instead, the cornea is in direct contact with water having index of refraction n(w)=1.33, its power is
The cornea has lost 41.2 diopters (87%) of its refracting power! This means that, underwater, the eye becomes severely hyperopic (or hypermetropic), so that parallel rays of light entering the relaxed eye are no longer brought to a focus on the retina, but well behind it (see below) so that everything is a blur.
P(w)={n(c)-n(w)}/R
= 6.3 diopters
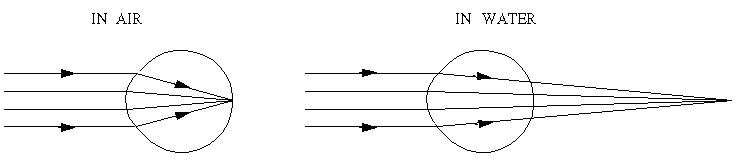
Clearly, the unaided eye is a rather poor tool in an underwater environment The earliest attempts to see 'normally' underwater probably involved clasping the hands tightly over the forehead and trapping an air bubble over the eyes. This works, but is certainly not convenient. The most popular modern 'fix' for this problem is the use of a face mask. It places the eye(s) behind a planar water/air interface (the glass or plastic plate is thin enough to be a negligible optical perturbation), and thus restores the normal functioning of the cornea. The mask does produce some problems of its own, however:
(i) refraction at the planar water/air interface causes objects to seem closer and bigger than they really are
(ii) the apparent magnification is a function of the angle of incidence at the interface, thus causing a 'pin-cushion' distortion at the periphery of vision
(iii) it reduces the binocular field of view from about 180 degrees in air to no more than 97.2 degrees in water, because of total internal reflection at the water/air interface (see the article entitled 'Total Internal Reflection').
REFERENCE:
F. R. Hallett, P. A. Speight, and R. H. Stinson, "Introductory Biophysics" (Methuen 1977), Chapter 3.