Field of View at a Planar Interface

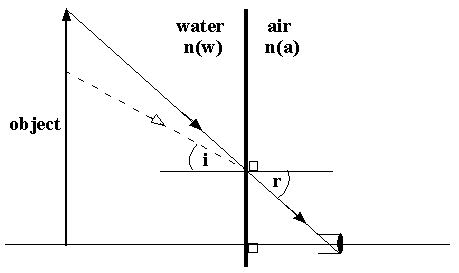
The angular field of view of a lens facing a planar air/water interface is less than its field of view in air. In the figure below, an object is shown which exactly fills the lens' in-air half-angle of view 'r'. The limiting light ray has been drawn from the top of the object to the lens. When the same object is immersed in water, rays from the top of the object can no longer reach the lens, because they are refracted away.

As you examine object points progressively further from the top of the object you will eventually find one such that a ray from it to the interface will refract along the same path as the limiting ray in air. The angle 'i' this ray (dashed line) makes with the normal to the interface must be consistent with Snell's Law, namely

sin(i) = [n(a)/n(w)]*sin(r)

where n(a) and n(w) are the indices of refraction, respectively, of air and water.

Since the ratio n(a)/n(w) is approximately 0.75, angle 'i' is always smaller than angle 'r', and the lens' effective field of view is smaller. If the lens is very close to the interface, its effective angular field of view is '2i'. Some typical values are shown below (angles in degrees).


in-air angular field of view:    180   140   100   60  30
in-water angular field of view:   97    90    70   44  22

For example, the underwater field of view of a 180-degree 'fisheye' lens is only 97 degrees behind a plane port.