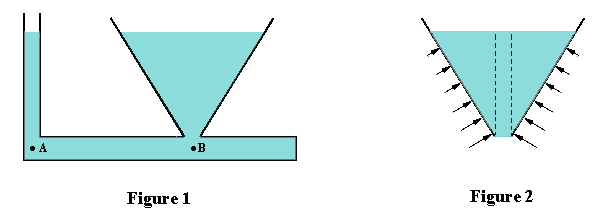The Hydrostatic Paradox

Before the principles of hydrostatics were understood, the behaviour of liquids was often very puzzling. For example, Figure 1 shows a vessel with two interconnected chambers which are open at the top and have bottom openings with the same cross-sectional areas. If you pour water into either chamber, it flows up into the other one until the water levels in both are identical. Is this not a paradox? Surely the chamber containing the larger volume of water must have a greater force per unit area at its base, and shouldn't this make the water in the smaller chamber rise to a higher level?

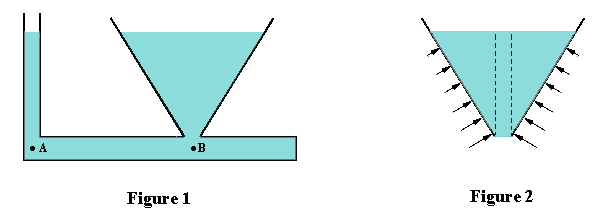
Blaise Pascal asked this question nearly 300 years ago. He even built an apparatus, now known as 'Pascal's vases', to demonstrate the paradox. It was basically the vessel shown in Figure 1 with several more differently shaped chambers, but all open at the top and having the same base areas. In fact, if Pascal's vases are generalized to include compartments with any shapes, inclinations, or different base areas, the results will always be the same: the water levels in all chambers will be identical.

This apparent paradox can be easily resolved by the application of some elementary mechanics. The pressure at a point in a static liquid is due entirely to the weight of liquid (plus the atmosphere) directly above it. This is clear from Figure 2, which shows the forces exerted by the walls of the chamber on the water above them. The forces are perpendicular to the walls, but their vertical components support the water. Only the column of water directly above the bottom opening contributes to the pressure at the base of the vessel. As explained in the article 'Hydrostatic Pressure at a Point', the pressure at any point in a liquid is the same from all directions. In Figure 1, consider the two points A and B which are in the same horizontal plane. For translational equilibrium in the horizontal direction, the horizontal pressures at points A and B must be identical. Otherwise there would be flow. Since the vertical pressures at A and B must be the same as their corresponding horizontal pressures, the heights of the water columns above A and B must be the same.

An even more striking paradox is that associated with the horizontal pressures on a dam. Consider Figure 3a, which shows a stylized version of the Hoover dam holding back Lake Mead.

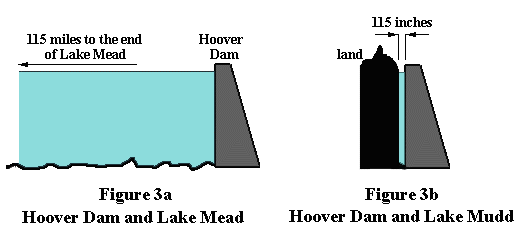
The lake is about 115 miles long and at the dam is about 600 feet deep. Near the dam's base the horizontal thrust is about 18 tons per square foot. Now have a look at Figure 3b, which shows the same dam holding back Lake Mudd, which is only 115 inches long. Here's the paradox: in both cases, the horizontal thrust on the dam is the SAME.

The explanation follows the same reasoning as above: the horizontal pressure at a point must be equal to the vertical pressure, but the vertical pressure depends only on the depth of the water, not on its horizontal extent. This can be easily demonstrated in the classroom by means of the apparatus shown in Figure 4. It consists of a glass container fitted with a flexible vertical membrane which separates it into a small chamber and a large chamber.

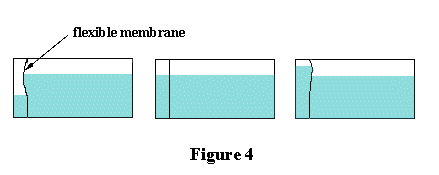
If water is poured into the large chamber the membrane will bulge out into the small chamber. Progressively adding water to the small chamber will make the bulge diminish, until it disappears entirely when the water levels on both sides of the membrane are the same. At this point the horizontal pressures exerted by the small and large volumes of water are identical. Continuing to add water to the small chamber will cause the membrane to start bulging in the direction of the large chamber.

F. W. Sears, M. W. Zemansky, and H. D. Young, "University Physics", (Addison-Wesley, 1976), Chapter 12.

Last Modified: 06:58pm , March 18, 1997