Water Wave Celerity

The three-dimensional behaviour of surface water waves as they interact with wind, bottom, obstructions, currents, and each other is very complex. Much insight into the general behaviour of waves can be obtained by first studying two-dimensional, monochromatic, progressive waves using the so-called small amplitude wave theory. The figure below defines the terms most commonly used in discussions of water waves:.

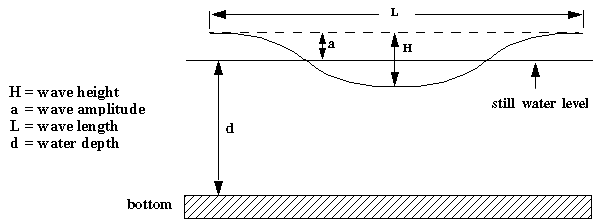
As waves pass some fixed point, the time between consecutive crests is the wave period T. The speed of the wave, or its celerity, C, (as ocean engineers refer to it), is the distance travelled by a crest per unit time, or

C = L/T                                            Equation 1

The small amplitude theory requires that both a/L and a/d be small. Using this assumption and solving the equation of motion for small amplitude waves yields the following expression for the wave celerity:

where g is the gravitational acceleration.

It is clear from Equation 2 that the wave celerity is a function of both the wave length (L) and the water's relative depth d/L. Since the hyperbolic tangent function (tanh) has simple limiting forms for both small and large values of its argument, it is useful to classify waves according to the relative depth, as follows:

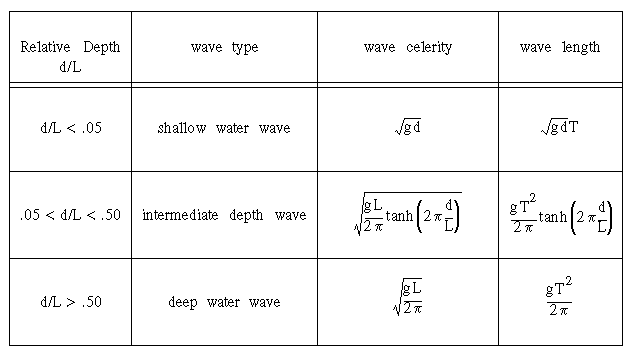
Note that in deep water the celerity is independent of water depth, which is not surprising in view of the fact that the waves do not interact with the bottom. What is interesting, however, is that the celerity depends on the wave length. Water is therefore a dispersive medium with respect to deep water surface waves, in much the same way that it is a dispersive medium for light waves. Shallow water surface waves, on the other hand, do feel the bottom, and slow down as the square root of the depth. Their speed is not a function of the wave length.

As surface waves travel across various depths of water their period T does not change (for a proof see the article entitled "Constancy of Wave Period"). In deep water, therefore, the wave length is constant, but as waves approach a beach the wave length decreases as the square root of the depth.

Wind-generated waves typically have periods from 1 to 25 seconds, wave lengths from 1 to 1000 meters, speeds from 1 to 40 m/s, and heights less than 3 meters. Seismic waves, or tsunamis, have periods typically from 10 minutes to one hour, wave lengths of several hundreds of kilometers, and mid-ocean heights usually less than half a meter. Because of their long wavelengths, tsunamis often satisfy the criterion for shallow-water waves. For example, when a tsunami with a wave length of 200 km passes over a depth of 4 km (the average depth of the oceans) the relative depth is d/L=.02. Since this is less than .05, this tsunami is a "shallow-water wave", and its celerity depends only on the water depth.

REFERENCES:

Robert M. Sorensen, "Basic Wave Mechanics for Coastal and Ocean Engineers" (John Wiley & Sons, 1993), Chapter 2..

Last Modified: 10:11pm , April 28, 1997