External Reflection from a Water Surface

Light is a transverse electromagnetic wave, meaning that it consists of mutually perpendicular oscillatory electric and magnetic fields which are both perpendicular to the direction of propagation. In the most general case the electric field vector periodically changes direction and magnitude as it rotates around an ellipse, i.e. it is elliptically polarized. This can always be thought of as the superposition of two independent oscillations, with the same frequency, along mutually perpendicular lines with fixed orientations in space. Each of these oscillations is referred to as plane polarized, with the plane of polarization being the one containing both the line of oscillation and the direction of propagation.

When a wave of visible light travelling through air strikes a water surface its incident energy is partially reflected from the surface and partially transmitted into the water. The fraction of the incident intensity (which is energy per unit area per unit time) that is reflected, i.e. the reflectance, depends strongly on the angle of incidence 'i' (see the figure) and the wave's polarization. The dependence on the light frequency (dispersion) is comparatively weak.

The application of Maxwell's equations of electrodynamics to this situation leads to rather simple expressions for the reflectances of waves with polarizations either perpendicular to or parallel to the plane of incidence. This is the plane containing the incident ray, reflected ray, refracted ray, and the normal to the surface at the point where the incident ray strikes it. In the figure shown below the reflectance for each direction of polarization has been plotted as a function of the angle of incidence.

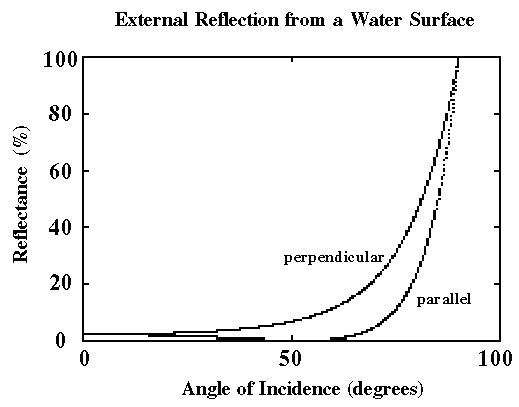
It is clear that at normal incidence (i=0 degrees) 98% of the light is transmitted into the water, while at grazing incidence (i=90 degrees) both polarization components are almost completely reflected. Since a wave with arbitrary polarization can be decomposed into a "perpendicular" component and a "parallel" component, its reflectance curve will be a weighted sum of the curves shown. In particular, if light is randomly polarized (natural sunlight) the average electric field components in all directions are the same, and the total reflectance is the average of the parallel and perpendicular reflectances.

Of special interest is the fact that the reflectance for the parallel component nearly vanishes at some intermediate angle of incidence. For a perfectly smooth surface the reflectance would be exactly zero. However, because of a small amount of non-specular reflection due to thermal agitation of the water molecules, the minimum reflectance is of the order 0.01%. The condition for a minimum is that the reflected and refracted rays be 90 degrees apart, which according to Snell's Law of refraction requires that:

tan(i) = n(w)/n(a)

This is known as Brewster's Law, and the angle it yields is called Brewster's angle, or the "polarizing angle". At this angle (53 degrees) the reflected ray is almost completely plane polarized and can therefore be almost totally quenched by an appropriately oriented polarizing filter. Moreover, the figure shows that the reflected light contains primarily the perpendicular component of polarization for a significant range of angles centered on the polarizing angle. This explains why polaroid sunglasses are so effective in eliminating glare from the surface of water.

J. D. Jackson, "Classical Electrodynamics" (John Wiley and Sons 1962), Vol. 1, Chapter 7.

F. A. Jenkins and H. E. White, "Fundamentals of Optics" (McGraw-Hill 1957), Chapter 25.